The Search for a Better Digital Elevation Model

• COP30 is a game changer, considering its global coverage, very good accuracy and free & open licence. Applications benefitting from it include satellite image correction, water flow modelling, 3D visualization and precision farming.
• COP30 is an upgrade to SRTM, because COP30 has better vertical accuracy, it's globally consistent, and it's newer.

Quality is a function of how the DEM will be used. For us, a DEM must identify obstructions that can interfere with radio signals. This means, in forested area, DEM elevations measure along tree tops and not the terrain below. And, for a hill, DEM elevations measure its top accurately; its slope is irrelevant. Contrast this with flood analysis, where terrain elevation — not tree top elevation — and slope are important.

The sections below document our methodology and results comparing SRTM with COP30.

Scenarios

Here are the results from comparing SRTM and COP30 to our 138 million vertical benchmarks. (We included NASADEM and FABDEM, two DEMs derived from SRTM and COP30.)

COP30 RMSE values are no better than SRTM, worse than NASADEM and much worse than FABDEM. What happened? RMSE is very sensitive to large errors. COP30's shorter radar wavelength ( 3.1 cm vs SRTM's 5.6 cm ) reflects higher in the canopy, acquiring an elevation far above the terrain elevation from the vertical benchmark. In short, COP30's high RMSE values in forested areas contaminated its global RMSE value.

To minimize this contamination, we segment our analysis by land cover type. Because the two radar wavelengths interact with sloped areas differently, we segment a second time by terrain slope. And, finally, we segment a third time by quadrant, dividing the continental United States into north-west, north-east, south-west and south-east quarters. 14 land cover types times 3 slopes times 4 quadrants equals 168 scenarios. We expect each DEM to respond differently to each scenario, with COP30 winning some and SRTM winning others. In short, there will be no overall winner. There can't be — to find one, is like trying to find the winning ice cream? chocolate or strawberry.

Interpolation Methods — Linear, Cubic or Spline?

SRTM and COP30 supply a ~ 30m grid of surface elevations, north to south and east to west. The elevation at a location is obtained by first translating the location to a grid cell and offset within that cell, and then interpolating the elevations at that cell with that of nearby cells, based on the offset.

Common interpolation methods include linear, cubic and spline. The window of adjacent cells to interpolate varies by method: 2x2 for linear, 4x4 for cubic or spline, or 6x6 for spline. Which interpolation method provides the most accurate results?

Because the two radar wavelengths interact with sloped areas differently, we segment a second time by terrain slope. And, finally, we segment a third time by quadrant, dividing the continental United States into north-west, north-east, south-west and south-east quarters. 14 land cover types times 3 slopes times 4 quadrants equals 168 scenarios.

We tried four interpolation methods (linear, cubic, spline4x4 and spline6x6) across 1,008 scenarios:

• 6 DEMs (SRTM, COP30, NASADEM, FABDEM, NASADEM HGTS* and COP30_I**).
• 3 slopes
• 4 quadrants in CONUS
• 14 NLCD landcover types

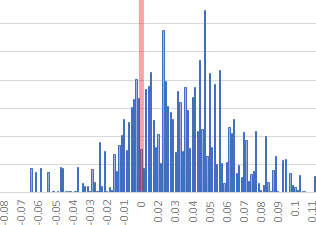
The x-coordinate of the graphs below represent [ RMSE_otherInterpolation - RMSE_linear ]. The y coordinate measures how many of the 1,008 scenario & DEM combinations had that RMSE difference The red line represents where the other interpolation method achieves parity with linear; to its right is where linear is stronger and to its left is where linear is weaker.

All three graphs show that all interpolation methods are within 0.1m RMSE — well within the margin of error for the vertical benchmarks. The graphs show a small bias, favoring linear (85% for; 15% against), and for that reason we chose to use linear for our analysis. Linear also uses the fewest CPU resources of the four.

* NASADEM HGTS is a float32 variant of NASADEM with WGS84 elevations. ** COP30_I is COP30 with grid cell elevations rounded to the nearest integer.

Linear vs Cubic

Linear vs Spline (4x4 window)

Linear vs Spline (6x6 window)